Et voilà une matrice de translation :

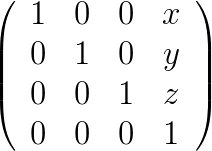
Où le vecteur :

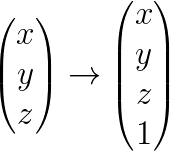
Qui est en fait un vecteur à quatre dimensions (pour rester cohérent avec les matrices 4x4) . Correspond à un déplacement du repère de (x, y, z).

Si vous n'êtes pas convaincu que ça fonctionne, nous pouvons faire le calcul à la main, prenons notre matrice que nous appellerons A et faisons la agir sur un vecteur position p = (x, y ,z, 1), le 1 étant la pour rester cohérent :

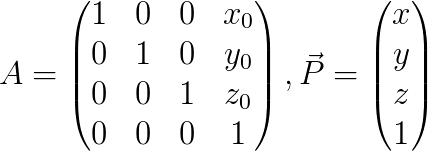
Faisons agir A sur P :

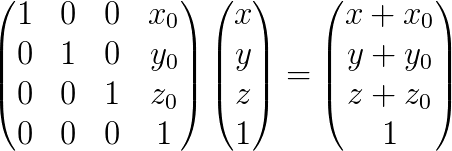
Ce qui donne bien :

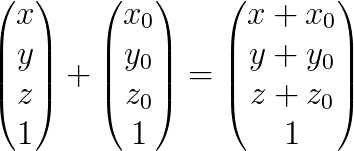
Heu, ce n'est pas un peu compliqué de passer par une matrice pour faire une simple addition ?

Sur le coup ça peu vous paraître compliqué, mais en fait ce qui importe c'est la rapidité de calcul.

Ben, oui, mais c'est plus compliquer de multiplier une matrice que d'additionner deux vecteurs ?

Et bien non, en tout cas pour votre carte graphique, et comme c'est elle qui va faire tout les calculs...

En effet, une carte graphique peut faire ce que l'on appel du calcul vectoriel, c'est-à-dire du calcul sur des vecteurs et non pas sur les coordonnées de ces vecteurs, de plus le calcul de multiplication de matrice est optimisé dans la carte elle-même. Donc nous avons tout intérêt à utiliser les techniques les plus rapide, car nous allons faire des millions de calculs par seconde (enfin la carte graphique et le processeur, pas nous).

C'est pour cela que toutes les transformations que je vais vous montrer se font à partir de multiplication de matrice.