Francais
The "pertuisanier"
One of the most beautiful...During the first world war, the body of a "pertuisanier" was unburied by a bomb. Knowing that 225533 is the product of:
1) Half of the age of the captain who leaded the battle where was dead the "pertuisanier"
2) the length of a "pertuisane" in feet
3) the last day of the month where the bomb exploded
4) the fourth of the difference between the year where exploded the bomb and the year where was dead the "pertuisanier"
What is the name of the uncle of the captain who leaded the battle where was dead the "pertuisanier"?
The french wine bottle of 25 FF
Three young Americans in Paris want to buy a french wine bottle. The price is 25 FF but they only have 10 FF each. They give thus 30 FF and wait for 5 FF back. But the seller has only 1FF coins. So, he decides to give back one 1FF coin to each guy and let 2 coins on the table. Conclusion. Each guy paid 10 FF - 1 FF = 9 FF, that is 27 FF, plus the 2 coins on the table: 29 FF. 1FF has disappeared. Is the seller honnest?...4 triangles with 6 matches
Take 6 matches and try, with the only action of placing the matches and without superposing them, to form 4 equilateral triangles.6 triangles with 6 matches
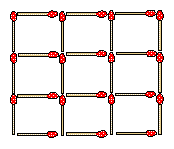(thank you to Bernard Werber and his book "Les Fourmis")
Same conditions as above, but you have now to give us 6 triangles !
8 triangles with 6 matches
(thank you to Bernard Werber and his book "Les Fourmis")Same conditions as above, but you have now to give us 8 triangles !
Still in the land of matches
On the picture aside made with 24 matches, take one match to get 10 squares. An other exercise: take 4 matches to get 4 squares. Or take 4 matches to get 5 squares. The play is to you.A hole through a sphere
You drill a cylindrical hole through a sphere. This hole is 6 cm long and is centered on the sphere's center. We suppose also that the diameter of the hole is less than its length. What is the volume of the rest of the sphere?The mathematical painter
Mr Math wants to pile up some cubes that he has first painted on the six faces. Those cubes are 1cm , 1/2 cm, 1/3 cm, 1/4 cm,... long. Will he succeed in piling up his cubes without reaching the roof? Will he find enough paint to paint them all?The logic of numbers
Here is a logical raw of numbers: 1, 11, 21, 1211, 111221, ... Can you find the next one?(some help: make your neuron become like a baby's one!)
Logic of letters
Here is a logical raw of letters: O, T, T, F, F, S, S, ... , ... Can you find the two following?The three sisters
The 3 daughters of Mr Dupont have a particularity:- the product of their ages is equal to 36
- the sum of their ages is equal to the number of the house at the other side of the street
When Mr Dupont tells this to the factor, this one looks back, see the number of the house and says that he lacks of information in order to find the ages of Mr Dupont's daughters. Then Mr Dupont says "the elder is blond!". Then, the factor, who is somewhat familiar with mathematics, find the solution.
Can you do the same?
Age and age
I have two times the age that you had when I had the age you have.When you will have the age I have, I will have two times the age you have.
What is my age?
The fly and the spider
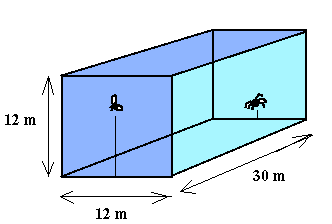Imagine a box as on the figure. A spider is at one side, a fly is at the other side.
The velocity of the spider is 0.5 km/h and looking at the dimension of the box, the
fly says that it can sleep for 5 minutes before the spider arrives. But the fly is wrong,
can you tell us why?...
A simple fly
Two trains are separated by 200 km. They come to meet each other at the celerity of 50km/h. A fly is flying at the speed of 75 km/h between the two trains, doing many go and return between the two, until the two trains meet. What total distance covered the fly?(one says that J. von Neumann was asked this question. After 10 seconds he gave the good answer. He was asked for his method and he said that he made the sum of the serie's terms!)
Money is not gold
You are in charge by your big boss to count his money and detect among his 500 bags the one which contains false golden coins. You have for that the weighting balance of the boss and he gave to you the permission of only one weighting! Only what you know is that a true golden coin weights 10 grams and a false golden coin weights 5 grams. There is at least one solution.A train exchange
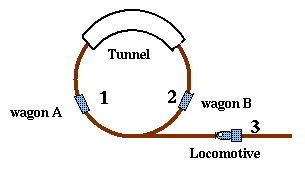The locomotive is in charge of exchanging the positions of wagon A and B, then coming
back to its departure position. It can go forward or backward but
it can pass only one time inside the tunnel.
Is there a solution?
A strange man
A man is living at the 25th floor of a 30 floors building. Each morning he takes the lift at the 25th floor down to the street and go to work. Each evening, he comes from his work and takes the lift up to the 24th floor before walking from the 24th up to the 25th. Why?The logic of Protagoras
In the antic Greece, a famous "jurist", Protagoras, was teaching to students and he accepted to teach to a very brilliant but poor one without asking him for money. After some years of teaching, he said to the student: "when you win your first suit, you must pay back!". The student did not accept and Protagoras engaged a suit against him.Protagoras said: "If he wins the suit, he will win his first suit so he must pay to me. If he looses this suit, he must pay to me. It's clear: he must pay!"
His student said: "If I win this suit, I don't have to pay to Protagoras. If I don't win this suit, it's not my first winned suit and I have not to pay to Protagoras. Thus, it's clear: I don't have to pay!"
Who is right?
The crossed ladders
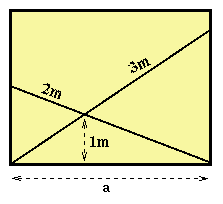The picture aside shows two ladders placed in a corridor of width a.
One of the ladder is 2 meter long. The other is 3 meter long.
The cross point of the ladders is at a height of 1 meter.
Can you find the value of a?
The logic of mathematics is crazy
So crazy that I don't remember...Improbable probabilities
Let F(a) be the probability that a random variable X is less than "a": F(a)= P(XThat is to say: P(a<=X
The celerity of snails
A snail is moving on a hypothetical elastic road which can dilate infinitely. The animal is at the beginning of the elastic road, moving at 1mm/s. The elastic road is 1km long at the beginning and is extending at the speed of 1km/s.I say that snail will catch the end of the road in a finite time. If you believe me, can you say how many time it will need to do so?
Wine and Water
A friend of you is tasting some wine. He has a 10cl glass of wine. You have glass with 10cl of water. You decide to take some of his wine in your glass. You mix 3cl of his wine with the 10cl of your water. But you want him not to see that you have stolen some wine, you take your mixture and put 3cl of it into his glass. Then you are sure that you have more wine in your glass than he has water in his glass. But are you wright?A camel story
Sure you know that one... A nomad is at the end of his life. He want to let to his 3 sons all what he has, that is a herd of 11 camels. He wants to give 1/2 to his elder, 1/4 to his cadet and 1/6 to his youngest son. But this is impossible with 11 camels. You, the nomad from the far mountains, are called and you come soon on your camel to solve the problem.How can you help him ?
Black and white hats
(Thanks to Frederic Faure)The great Sultan has to replace his vizier. Three candidates are presented. He wants his new vizier to be cleaver and make a trick to find the most cleaver one. He places them in a row, so that the third one can see the head of the two preceding him, the second can see the head of the first one and the first can see nothing. Then, he says to the three candidates that he has five hats: 3 black and 2 white. He passes behind them and put, randomly, one hat on each head. Then, he asks them what colors are their own hat. After some seconds of silence,
the last of the row answers: "I don't know...",
the second one answers: "I don't know..."
Then, the first of the row answers: "I know! The color of my hat is..."
How did he find and what is the color of his hat?
The two locomotives
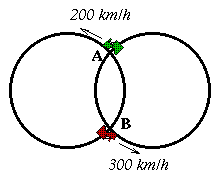On two circular iron ways of radius R and whose centers are distant
of D, two locomotives are traveling at the speed of 200 km/h and
300 km/h respectively. The start together, from the points A and B
respectively. When will they meet at point A or point B?
Mice in flat Land
(Thanks to Jerome Damet)Three mice are living in a special world were all is flat. Everywhere they can go, there is only a flat ground until infinity, in every direction. Moreover, those mice are always running and always in a row. The first one says: "I am a little mouse and I am followed by two little mice!", the second one says: "I am a little mouse and I am followed by one little mice!" and the third one says: "I am a little mouse and I am followed by two little mice!".
How is it possible??
The english cochonnet
(Thanks to Jerome Damet)Difficult to give in English, because it contains french words jokes. The game of english cochonnet is played at 3, not at 3 out of jail or at 3 in the forest, but at 3 1,2,3! The first player takes the ball and throws it, the second takes the javelin a the ball. What does the third player?
English original version (thanks to Francois Desarmenien):
What is "le petit cochonnet anglais"?
"Le petit cochonnet anglais" is a french game with 3 players:
-- the first takes the ball and throws it,
-- the second takes the throw and the ball,
-- the third is "le petit cochonnet anglais".
But what is "le petit cochonnet anglais"?
"Le petit cochonnet anglais" is a french game...
Etc, etc...
The square of the fool
On the figure below are drawn 9 stars. You must pass on all of them with your pen by a continuous line (without raising your pen) and using only 4 direction's changes.
* * *
* * *
* * *
The circle of the fool
In the same spirit, but even more difficult. Take a sheet of paper and draw on it a circle and its center without raising your pen.Additions with letters
To each of the letters below is associated one number and only one between 0 and 9. Knowing that the additions below are right and uncorrelated, can you find the numbers corresponding to the letters?
TWENTY
+ TWENTY
+ TWENTY
+ TEN SEND
+ TEN + MORE
---------- -------
EIGHTY MONEY
A coin game
A magician who likes statistics, is asked by the king to find him a new mathematician. Two young men are candidates. He thus asked them the following question:"You have a coin with face 1 and face 2. You throw it ten times. How many results can you obtain?..."
The first one answer: "You throw ten times, so you get ten results!"
The second one answer: "You can get 0 time face 1 and 10 times face 2, or 1 time face 1 and 9 times face 2, or..., 10 times face 1 and 0 time face 2. So, you have 11 possible results!"
Who is right?
Dwarfs and Giants
You have 3 large 5 dollars coins and 2 small 1 dollar coins.Beginning position: GsGsG (G for Great and s for small).
With only 3 moves, that is 3 translations of a group of 2 neighboring coins, you must obtain the following result: ssGGG
More difficult:
With only 5 moves, that is 5 translations of a group of 2 neighboring coins Gs or sG (the moves GG of ss being strictly forbidden!!), you must obtain the following result: GGGss
The fool of the king
Almost impossible to translate in English, but let's try... The fool of the king is sir-tea fool. He carries a full inside which are the seals of the king. The fool stumbles and the fine fool falls. How many fools and seals was there? Where are the two others?Some clever ratios
Find the numerical value of the following ratios:ROSSINI CHEVAL ------- ------ SOLSIDO OISEAUAlso, demonstrate the following equality:
VERT ------- = CASSOULET KROUMIR
A nice logic
You certainly know that if you have two propositions P and Q with P => Q , than you can deduce that no Q => no P. Here is a fine example:If it is possible to touch a clock without stopping it, it certainly can be possible to start a clock without touching it!...
A variant is: If you can stop the run without seeing a nu_tau, then you can see a nu_tau without starting the run!...
A logical mistake
A little in the same way, knowing that ( P => Q ) is a logical proposition equivalent to ( no P or Q ), one can write that ((P=>Q) or (Q=>P)) is equivalent to ((noP or Q) or (noQ or P)) that is ((noP or P) or (noQ or Q)) which is always true. And that whatever are P and Q.To you to find examples...
An other logical mistake
In the proposition ( P=>Q )let's take P=noQ, one has then ( noQ => Q ) which is equivalent to ( no(noQ) or Q) that is (Q or Q) which is equivalent to Q. The principle of excluded tiers tells us that ( noQ => Q ) is always false. Thus, from what preceeds, Q is always false, whatever it is!Logic and kindness
Two gentlemen are at the restaurant. They have ordered fish. The waiter comes with a plate containing two fishes: a big one and a little one. The first man very kindly says to the other: "Please, take it first." and the other gentleman takes the biggest fish. The first man says: "Shocking! If I were asked the take first, I would have take the little one!". And the other answers: "Why are you crying! You have what you would have taken!"Any triangle is isocel
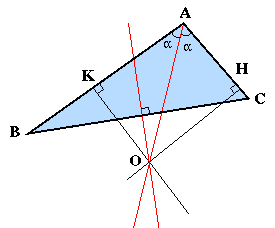(Thanks to Remy Lafaye)Thanks to Remy, I can give you this nice mathematical mistake. The figure beside shows you a common triangle where the red lignes are the bisector of (AC,AB) and the mediatrice of BC. Their intersection is the point O and the orthogonal projection of O onto AC and AB are the points H and K. So, we can already say that OH=OK and AH=AK (bisector) and that OB=OC (median). Then, from Pythagore theorem, we can say that HC=KB. Since AH=AK and HC=KB, we conclude that AH+HC = AK+KB, that is: AC=AB. Every common triangle is isocel. Obviously not! Did you find the mistake?
The irreducible triangle
... to completeAn other irreducible triangle
... to completeA strange triangle
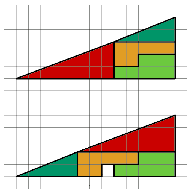(thanks to Vivek SenGupta who sended it to me).
A triangle is made of 4 pieces.
One move the pieces and rebuild the triangle.
Oh! Something is missing! How is it possible?
The U2 bridge
(thanks to Vivek SenGupta who sended it to me).The rock band U2 having 4 members are to give a concert in 17 minutes. They have to cross a rope bridge within that time or else they will be late. The bridge can hold maximum 2 people at any given time. It is night and dark, so they have one torch which must always be with the people crossing the bridge at any time. The 4 members can cross the bridge in individual times of 10 minutes, 5 minutes, 2 minutes and 1 minute. But, when 2 people cross the bridge, they together take the time of the slower person. For example, if first 2 members (having times 10 and 5 minutes) cross together then they take 10 minutes. How can they cross in 17 minutes so that they are not late for the concert?
One climb for 3 lights
(thanks to Vivek SenGupta who sended it to me). You are on the ground floor of a building. There are 3 light switches in front of you, and the corresponding light bulbs are on the 1st floor. Initially all the light bulbs are off. By going up to the 1st floor just once, you must identify which switch corresponds to which light bulb. Assume that you can not see the light bulbs from the ground floor and that the question makes sense, i.e. light bulbs are not connected in serie.The self-refering sentences
No paradoxe: "This sentence contains five words"Infinite loop: "The sentence says that this sentence says that..."
Paradoxe: "This sentence is false"
I let you think about that...
The strange little i
Let "a" be a real positive number. The saquare root of a noted sqrt(a) is equal to sqrt(a*i*i*i*i) since the imaginary number i squared is equal to -1. By putting out the i to the 4 from the square root, you obtain:sqrt(a) = i*i*sqrt(a) = - sqrt(a).
What have we forget?
Fraction is running
Consider the fraction (2/3) / (2/5). It is equal to (2/3) x (5/2) that is 5/3. But it is also equal to ((2/3)/2)/5 that is (1/3)/5 that is 1/15.Where is the mistake (easy!)?
The King Pepin (You have to know french language!)
This is the story of the King PEPIN:ROI PEPIN G | __|Have you find what is the sad story of king Pepin?
The ill monks
In a monastry, the main monk remarks that some of his monks are subject to an incurable and deadly illness. This illness is caracterized by a red spot between the eyes. Since he does not want to take the risk of a contagion in the monastery, he stops the usual silence and says a small talk in which he asks to the ill monks to leave the monastry as rapidly as possible.To respect this commandement is a bit complex:
1. The main monk does not say which monk is ill.
2. The monks must not communicate with each other.
3. The monks must not look themselves in some mirrors or to examine themselves in any way.
4. The monks must live in their cellules and see each other only one time per day during the general priest.
We consider also that:
1. The illness makes no more victims during this preparation of departure of the currently ill monks.
2. All the monks have the same level of intelligence.
3. All the monks are honnest and obedient.
How many days will be needed for all the ill monks to leave the monastery?
Back to my page
Didier Verkindt . . .
LAPP