English
Le pertuisanier
Une des plus belles...Au cours de la premiere guerre mondiale, un obus deterre le corps d'un pertuisanier. Sachant que 225533 est le produit de:
1) la moitie de l'age du capitaine qui commandait la bataille durant laquelle est mort le pertuisanier
2) la longueur en pieds d'une pertuisane
3) le dernier quantieme du mois ou l'obus a eclate
4) le quart de la difference entre l'annee ou l'obus a eclate et l'annee ou est mort le pertuisanier.
Quel est le nom de l'oncle du capitaine qui commandait la bataille ou est mort le pertuisanier?
La bouteille de vin de 25 francs
Trois jeunes americains a Paris veulent acheter une bouteille de vin francais. Le prix est de 25 FF mais ils n'ont que 10 FF chacun. Ils donnent donc 30 FF et attendent 5 FF de monnaie. Mais le barman n'a que des pieces de 1 FF. Il decide donc de rendre 1 FF a chacun et laisse 2 pieces sur la table. Conclusion: chacun a paye 10 FF - 1 FF = 9 FF, ce qui fait 27 FF, plus les deux francs sur la table: 29 FF. 1 FF a disparu. Le barman est-il honnete?...4 triangles avec 6 allumettes
prenez 6 allumettes et essayez, en ne faisant que placer les allumettes sans les superposer, de former 4 triangles equilateraux.6 triangles avec 6 allumettes
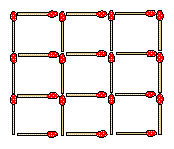(merci a Bernard Werber et son livre "Les Fourmis")
Meme conditions que precedemment, mais essayez maintenant de faire 6 triangles equilateraux!
8 triangles avec 6 allumettes
(merci a Bernard Werber et son livre "Les Fourmis")Meme conditions que precedemment, mais essayez maintenant de faire 8 triangles equilateraux!!
Toujours au pays des allumettes
Sur le dessin ci-contre fait avec 24 allumettes, enlever une allumette pour avoir 10 carres. Autre exercice: enlever 4 allumettes pour avoir 4 carres. Ou encore enlever 4 allumettes pour avoir 5 carres. A vous de jouer.Un trou dans une sphere
Vous percez un trou cylindrique a travers une sphere. Ce trou fait 6 cm de long et suit un diametre de la sphere. On suppose d'autre part que le diametre du trou est inferieur a sa longueur. Quel est le volume restant de la sphere?Le peintre mathematique
Monsieur Math veut empiler des cubes qu'il aura auparavant peint sur leurs 6 faces. Ces cubes sont de longueur 1cm , 1/2 cm, 1/3 cm, 1/4 cm,... Parviendra-t-il a tous les empiler sans toucher le plafond? Aura-t-il suffisamment de peinture pour les peindre tous?La logique des nombres
Voici une suite logique de nombres: 1, 11, 21, 1211, 111221, ... Pouvez-vous trouver le suivant?(un peu d'aide: demandez a vos neurones de redevenir simples comme ceux d'un bebe!)
La logique des lettres
Voici une suite logique de lettres: U, D, T, Q, C, S, S, ... , ... Pouvez-vous trouver les deux suivantes?Les trois soeurs
Les 3 filles de Mr Dupont ont une particularite:- le produit de leurs ages est egal a 36
- la somme de leurs ages est egal au numero de la maison d'en face. Lorsque Mr Dupont dit cela au facteur, celui-ci se retourne, voit le numero de la maison d'en face et dit qu'il lui manque une information pour trouver l'age de chacune des filles. Alors Mr Dupont dit "l'ainee est blonde!". Alors, le facteur, qui est un peu matheux a ses heures, trouve la reponse.
Pouvez-vous en faire autant?
Age et age
J'ai deux fois l'age que tu auras quand j'aurai l'age que tu as.Quand tu auras l'age que j'ai, j'aurai deux fois l'age que tu as.
Quel age ai-je?
La mouche et l'araignee
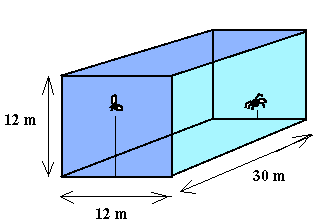Imaginez une boite comme sur la figure ci-contre. Une araignee est sur une des faces, a 1 metre
du sol. La mouche est sur la face opposee, a 1 metre du plafond.
La vitesse de deplacement de l'araignee est de 0.5 km/h
et d'apres les dimensions de la boite, la mouche se dit qu'elle peut dormir
tranquille pendant 5 minutes avant que l'araignee n'arrive sur elle.
Mais la mouche se trompe. Pourquoi?...
Une simple mouche
Deux trains sont separes de 200 km. Ils viennent l'un vers l'autre a la vitesse de 50 km/h. Une mouche vole d'un train a l'autre a la vitesse de 75 km/h, faisant des aller-retour reguliers entre les deux jusqu'a ce qu'ils se rencontrent. Quelle est la distance totale couverte par la mouche?(on dit que J. von Neumann, mathematicien, fut soumis a cette simple enigme. Apres 10 secondes, il donna la bonne reponse. On lui demanda alors comment il s'y etait pris et il repondit qu'il avait fait la somme des termes d'une serie!)
L'argent n'est pas de l'or
Vous etes charge par votre patron de compter son argent et de detecter parmi 500 sacs celui qui contient des fausses pieces d'or. Vous disposez pour cela d'une balance et le patron ne vous autorise qu'a une seule pesee!! Vous savez seulement qu'une vraie piece d'or pese 10 grammes et qu'un fausse pese 5 grammes. Il y a au moins une solution.Un tour de train
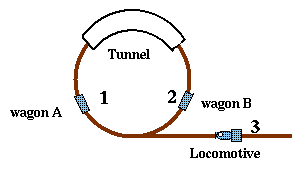La locomotive est chargee d'echanger les positions des wagons A et B puis de revenir a sa
position de depart. Elle peut aller en avant et en arriere,
mais elle n'a le droit de passer qu'une seule fois dans le tunnel.
Y-a-t-il une solution?
Un homme etrange
Un homme habitant le 25eme etage d'un immeuble de 30 etages, part chaque matin a son travail. Il prend l'ascenseur au 25eme etage et descend au rez-de-chaussee, puis se rend a son travail. Chaque soir, il revient, prend l'ascenseur au rez-de-chaussee et monte jusqu'au 24eme etage puis grimpe le dernier etage a pied. Pourquoi ce comportement?La logique de Protagoras
Dans la grece antique, un celebre "juriste", Protagoras, enseignait a des etudiants et il accepta de donner des cours a un brillant mais pauvre etudiant sans lui demander le moindre argent en echange. Apres quelques annees d'enseignement, il lui dit: "Si tu gagne ton premier proces, tu me rembourses tout ce que tu me dois." L'etudiant refusa et Protagoras engagea un proces contre lui.Protagoras dit: "Si il gagne ce proces, il aura gagne son premier proces et il devra donc me rembourser. Si il perd ce proces, il doit me payer. De toute facon, il me remboursera."
Son etudiant dit:"Si je gagne ce proces, je n'ai plus a payer Protagoras et si je le perd, je n'aurai toujours pas gagne de proces et je n'aurai donc pas a payer Protagoras. Dans tous les cas, je ne paie pas."
Qui a raison?
Les echelles croisees
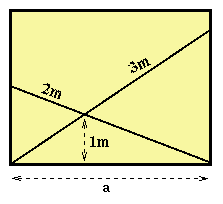La figure ci-contre montre deux echelles posees dans un couloir de largeur a.
L'une fait 2 metres de long, l'autre 3 metres.
Le point ou se croisent les deux echelles se trouve a 1 metre de haut.
Pouvez-vous trouver la valeur de a?
La logique des mathematiques est deroutante
Tellement deroutante que je ne m'en souviens plus!...Les probabilites improbables
Soit F(a) la probabilite qu'une variable aleatoire X soit inferieure a "a" : F(a) = P(X<a)On peut alors ecrire aussi: F(b) = P(X<b) et 1-F(a) = P(X>=a).
C'est a dire: P(a<=X<b) = F(b)*(1-F(a)) .
Mais quand "a" tend vers "b", F(a) tend vers F(b) et P(a<=X<b) tend vers F(b)*(1-F(b)) qui n'est pas nulle. Etonnant n'est-ce pas!
La vitesse des gasteropodes
Un escargot se deplace sur une hypothetique route elastique qui peut s'allonger indefiniment. L'animal se trouve au debut de la route elastique, se deplacant a 1mm/s. La route elastique fait 1 km de long au depart et s'allonge a la vitesse de 1km par seconde.Je dis que l'escargot atteindra le bout de la route en un temps fini. Si vous me croyez, pouvez-vous dire combien de temps mettra l'escargot a rattraper le bout de la route?
Mieux vaut boire le vin d'ici que l'eau de la
Un de vos amis goute un peu de vin. Il a un verre de 10 cl rempli de vin. Vous avez un meme verre rempli d'eau. Vous decidez (sacrilege!) de prendre un peu de son vin dans votre verre d'eau. Vous ajoutez 3cl de son vin a vos 10 cl d'eau. Mais vous ne voulez pas qu'il s'apercoive que vous avez vole un peu de son vin, vous prenez alors votre melange et en versez 3 cl dans son verre. Alors vous etes sur que vous avez plus de vin dans votre verre d'eau qu'il n'y a d'eau dans son verre de vin. Mais avez-vous raison? La reponse depend-elle de la quantite de vin ajoutee a votre eau (3 cl)?Une histoire de chameau
Je suis sur que vous la connaissez, mais bon... Un vieux nomade arrive a la fin de sa vie. Il desire laisser a ses fils tout ce qu'il possede, c'est a dire un troupeau de 11 chameaux. Il veut donner la moitie a son aine, 1/4 a son cadet et 1/6 a son benjamin. Mais cela est impossible avec 11 chameaux. Vous, le nomade des montagnes lointaines, etes alors appele pour aider le pauvre homme. Vous arrivez avec votre chameau.Comment pouvez-vous l'aider?
Chapeaux blancs et chapeaux noirs
(merci a Frederic Faure)Son altesse le Sultan doit remplacer son vizir. Trois candidats se presentent. Il veut que son nouveau vizir soit un homme intelligent et trouve une astuce pour le denicher. Il les fait aligner de facon que le troisieme voit la tete des deux qui le precedent, le deuxieme voit celle du premier et le premier ne voit rien. Puis, passant derriere eux, il dit aux trois candidats qu'il a cinq chapeaux: 2 noirs et 3 blancs. Il prend trois chapeaux et en met un sur chaque tete. Puis, il leur demande quelle est la couleur de leur chapeau. Quelques secondes de silence passent puis
le dernier de la file repond: "Je ne sais pas..."
le second repond: "Moi non plus..."
Alors, le premier de la file dit: "Je sais! La couleur de mon chapeau est...".
Comment a-t-il fait et quelle est la couleur de son chapeau?
Les deux locomotives
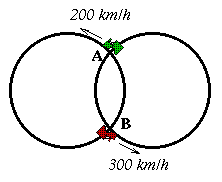Sur deux voies ferrees circulaires de rayon R et dont les
centres sont distants de D, deux locomotives circulent a la
vitesse de 200km/h pour l'une et 300 km/h pour l'autre.
Elles demarrent ensemble, l'une du point A, l'autre du point B.
Quand se rencontreront-elles en A ou en B?
Souris du plat pays
(Merci a Jerome Damet)Trois souris vivent dans un monde un peu special et completement plat. Ou qu'elles aillent, il n'y a qu'une grande plaine etendue a l'infini, dans toutes les directions. De plus, ces souris courrent tout le temps en file indienne. La premiere dit: "Je suis une petite souris et je suis suivie par deux petites souris!", la seconde dit: "Je suis une petite souris et je suis suivie par une petite souris!" et la troisieme dit: "Je suis une petite souris et je suis suivie par deux petites souris!".
Comment est-ce possible??
Le cochonnet anglais
(Merci a Jerome Damet)Le jeu du cochonnet anglais se joue a 3, non pas a 3 en Champagne ni a 3 en Asie Mineure mais a 3 1,2,3! Le premier prend la boule et la lance, le second prend la lance et la boule. Que fait le troisieme?
Version originale anglaise (merci a Francois Desarmenien):
Qu'est-ce que "le petit cochonnet anglais"?
Le petit cochonnet anglais est un jeu essentiellement francais qui se joue a trois:
-- le premier prend la boule et la lance,
-- le second prend la lance et la boule,
-- le troisieme est le petit cochonnet anglais.
Mais qu'est-ce que "le petit cochonnet anglais"?
Le petit cochonnet anglais est un jeu essentiellement francais...
Etc, etc...
Le carre du fou
Sur la figure ci-dessous sont dessines 9 etoiles. Passez par tous les points avec votre crayon d'un trait continu (sans lever le crayon) et seulement 4 changements de direction.
* * *
* * *
* * *
Le cercle du fou
Dans le meme filon, encore plus difficile. Prenez une feuille de papier et dessinez un cercle ainsi que le centre du cercle sans lever le crayon.Les additions lettrees
A chaque lettre ci-dessous est associe un chiffre et un seul. Sachant que les additions ci-dessous sont justes et sans rapport entre elles, pouvez-vous retrouver a quels chiffres correspondent les lettres?
TWENTY
+ TWENTY
+ TWENTY
+ TEN SEND
+ TEN + MORE
---------- -------
EIGHTY MONEY
Un jeu de pile ou face
Un mage qui aime les statistiques est requis aupres du roi pour lui trouver un nouveau mathematicien. Deux jeunes gens se presentent et le mage leur demande:"Vous avec une piece avec deux faces, la face A et la face B. Vous la lancez dix fois. Combien de resultats pouvez-vous obtenir?..."
Le premier repond: "On lance dix fois, donc on obtient dix resultats."
Le second repond: "Je peux obtenir 0 fois la face A et 10 fois la face B, ou 1 fois la face A et 9 fois la face B, ou..., 10 fois la face A et 0 fois la face B. Donc, j'ai 11 possibilites de resultats."
Qui a raison?
Les naines et les geantes
Vous disposez de 3 grosses pieces de monnaie (G) et 2 petites (p).Position de depart: GpGpG
En 3 mouvements, soit 3 translations d'un groupe de 2 pieces voisines, vous devez obtenir le resultat suivant: ppGGG.
Plus difficile:
En cinq mouvements, soit 5 translations d'un groupe de 2 pieces voisines Gp ou pG (les mouvements GG ou pp sont STRICTEMENT INTERDITS!!), vous devez obtenir le resultat suivant: GGGpp. Et en 4 mouvements seulement? Est-ce possible?
Le sot du Roi
Celle-la est plus a dire qu'a ecrire, mais bon... Le fou du roi est tres sot. Il porte un seau dans lequel se trouve les sceaux du roi. Le fou trebuche et l'etroit seau tombe. Combien y avait-il de sceaux? Ou se trouvent les deux autres?Quelques rapports astucieux
Trouver la valeur numerique des rapports suivants:ROSSINI CHEVAL ------- ------ SOLSIDO OISEAUEnfin, demontrez l'equation suivante:
VERT ------- = CASSOULET KROUMIR
Une belle logique
Vous conaissez certainement la regle suivante: si vous avez deux propositions P et Q telles que P => Q (P implique Q), vous pouvez en deduire que non Q => non P. En voici un bel exemple:Si il est possible de toucher une horloge sans l'arreter, alors il est certainement possible de demarrer une horloge sans la toucher!...
Une variante: Si vous pouvez arreter l'experience sans avoir vu un neutrino tau, alors il est certainement possible de voir un neutrino tau sans avoir demarre l'experience!...
Une erreur de logique
Un peu dans le meme genre, sachant que ( P => Q ) est une proposition logique equivalente a ( non P ou Q ), on peut ecrire que ((P=>Q) ou (Q=>P)) est equivalent a ((nonP ou Q) ou (nonQ ou P)) c'est a dire ((nonP ou P) ou (nonQ ou Q)) qui est toujours vrai. Ceci quels que soient P et Q.A vous de trouver des exemples...
Une autre erreur de logique
Dans la proposition ( P=>Q ) prenons P=nonQ, on a alors ( nonQ => Q ) qui est equivalent a ( non(nonQ) ou Q) soit (Q ou Q) qui est equivalent a Q. Le principe du tiers exclu nous dit que ( nonQ => Q ) est toujours faux. Donc, d'apres ce qui precede, Q est toujours faux. Ceci quel que soit Q !Logique et politesse
Deux gentlemen sont au restaurant. Ils ont commande du poisson. Le serveur arrive avec un plat contenant deux poissons: un gros et un petit. Le premier homme tres poliment propose a l'autre de se servir en premier. Et l'autre se sert et prend le plus gros poisson. Choque, le premier gentleman dit a l'autre: "Si on m'avais poliment offert de me servir en premier, j'aurais pris le plus petit, monsieur!"Et l'autre lui repond: "De quoi vous plaignez-vous! Vous avez ce vous auriez pris!"
Tout triangle est isocele
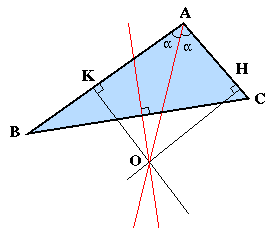(merci a Remi Lafaye)Grace a Remi, je peux vous offrir cette jolie erreur de mathematique. La figure ci-contre montre un triangle quelconque ou les lignes en rouge sont la bissectrice de l'angle (AB,AC) et la mediatrice de BC. Leur intersection est le point O et les projections orthogonales de O sur AC et AB sont les points H et K. Donc, nous pouvons deja ecrire OH=OK et AH=AK (bissectrice) et OB=OC (mediane). Alors, d'apres le theoreme de Pythagore, on peut en conclure que HC=KB. Puisque AH=AK et HC=KB, nous en concluons que AH+HC = AK+KB, c'est a dire AC=AB. Tout triangle est donc isocele. Evidemment non! Avez-vous trouve l'erreur?
Le triangle irreductible
... a completer...Un autre triangle irreductible
... a completer ...Un triangle bizarre
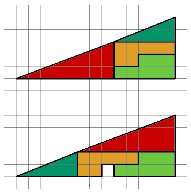(merci a Vivek SenGupta qui me l'a envoyee).
Un triangle rectangle est constitue de 4 morceaux.
On change les morceaux de place et l'on reforme le triangle.
Tiens! Il manque un bout! Comment est-ce possible?
Le pont de U2
(merci a Vivek SenGupta qui me l'a envoyee).Le groupe de rock U2, compose de 4 musiciens, doit donner un concert dans 17 minutes. Il doivent pour cela traverser un pont suspendu dans ce laps de temps, sinon ils seront en retard. Le pont ne peut supporter que 2 personnes au maximum. Il fait nuit et ils disposent d'une torche, qui doit toujours etre dans les mains de ceux qui traversent le pont. Les 4 musiciens traversent le pont en respectivement 1,2,5 et 10 minutes. Mais, si deux d'entre eux traversent ensemble, ils sont soumis au temps de traversee du plus lent. Par exemple, si Monsieur 10 minutes et Monsieur 5 minutes traversent le pont ensemble, il leur faudra 10 minutes. Comment peuvent-ils traverser en 17 minutes afin de ne pas etre en retard au concert?
Une montee et trois lampes
(merci a Vivek SenGupta qui me l'a envoyee). Vous etes au rez-de-chaussee d'un immeuble. Il y a trois interrupteurs devant vous et les lampes correspondantes se trouvent au premier etage. Initialement, toutes les lampes sont eteintes. En montant une seule fois au premier etage, vous devez determiner quel interrupteur correspond a quelle lampe. On suppose que les lampes ne sont pas visibles depuis le rez-de-chaussee et que la question a un sens, c'est a dire que les lampes ne sont pas connectees en serie.Les phrases auto-referentes
Non paradoxale: "Cette phrase contient cinq mots"Bouclage infini: "Cette phrase dit que cette phrase dit que..."
Paradoxale: "Cette phrase est fausse"
Je vous laisse mediter la-dessus...
L'etrange petit i
Soit a un nombre reel positif. La racine carree de a notee sqrt(a) est egale a sqrt(a*i*i*i*i) puisque que le nombre imaginaire i au carre est egal a -1. En sortant i*i*i*i de la racine, on obtient:sqrt(a) = i*i*sqrt(a) = - sqrt(a).
Qu'avons nous oublie?
La fraction est en action
Soit la fraction (2/3) / (2/5). Elle est egale a (2/3) x (5/2) soit 5/3. Mais elle est aussi egale ((2/3)/2)/5 soit (1/3)/5 soit 1/15.Ou est l'erreur (facile!)?
Le Roi Pepin
Ceci est l'histoire du roi PEPIN:ROI PEPIN G | __|Avez-vous trouve quelle est l'histoire triste du roi Pepin?
Les moines malades
Dans un monastere, le moine superieur remarque que certains de ses moines sont atteint par une maladie mortelle et incurable. Cette maladie est caracterisee par l'apparition d'une tache rouge sur le front. Comme il ne veut pas prendre le risque d'une contagion du monastere, il rompt le silence habituel et prononce un petit discours demandant aux moines malades de quitter le monastere, dans les plus brefs delais.Le respect a cette injonction est soumis a quelques regles:
1. Le moine superieur ne denonce pas les moines malades.
2. Les moines ne peuvent ni se parler ni communiquer.
3. Les moines n'ont pas le droit de se regarder dans le miroir ou de s'examiner de quelque maniere que ce soit.
4. Les moines vivent reclus dans leur cellule et ne se voient qu'une fois par jour, lors de la priere commune.
On considere:
1. La maladie ne fait pas de nouvelles victimes apres l'annonce du moine superieur.
2. Tous les moines possedent le meme niveau d'intelligence.
3. Les moines sont honnetes et obeissants.
Apres combien de jours les moines malades auront-ils tous quitte le monastere?
Back to my page
Didier Verkindt . . .
LAPP