6.3.4.1.1 : Cas classique
La figure 82 montre les performances obtenues avec un produit de matrices naïf lorsqu'il traite des tableaux initialisés ou non avec des nombres dénormalisés. On constate que la présence de nombres dénormalisés dégrade fortement les performances quand ceux-ci représentent entre
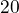 et
et 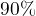 des valeurs traitées.
des valeurs traitées.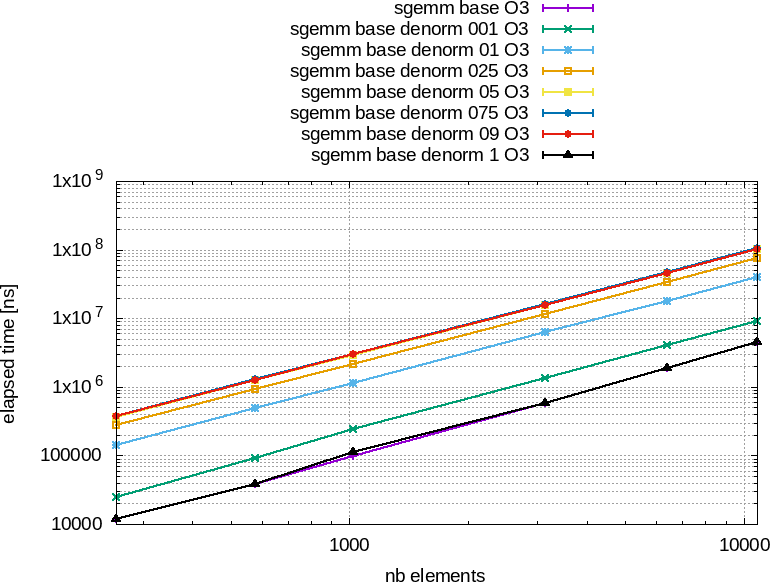
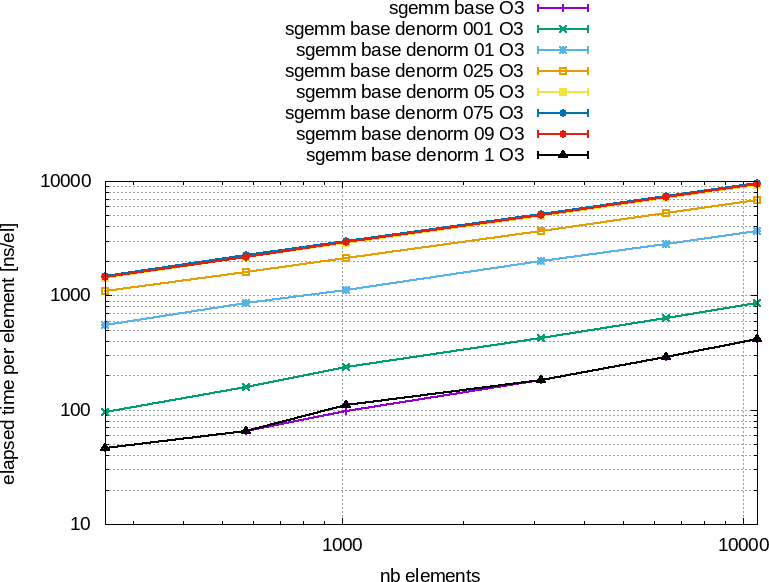
![]() Figure 82 : Performances obtenues avec l'optimisation -O3 entre un produit de matrices naïf (+ violet) et la même fonction mais sur des tableaux initialisés aléatoirement avec des nombres dénormalisés, entre 1 (001) et $100%$ (1).
À gauche, le temps total en nanosecondes en fonctions du nombre d'éléments.
À droite, le temps par élément en nanosecondes en fonctions du nombre d'éléments.
Figure 82 : Performances obtenues avec l'optimisation -O3 entre un produit de matrices naïf (+ violet) et la même fonction mais sur des tableaux initialisés aléatoirement avec des nombres dénormalisés, entre 1 (001) et $100%$ (1).
À gauche, le temps total en nanosecondes en fonctions du nombre d'éléments.
À droite, le temps par élément en nanosecondes en fonctions du nombre d'éléments.
La figure 83 montre les performances obtenues avec un produit de matrices lorsqu'il traite des tableaux initialisés ou non avec des nombres dénormalisés. On constate que la présence de nombres dénormalisés dégrade fortement les performances quand ceux-ci représentent entre
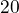 et
et 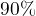 des valeurs traitées.
des valeurs traitées.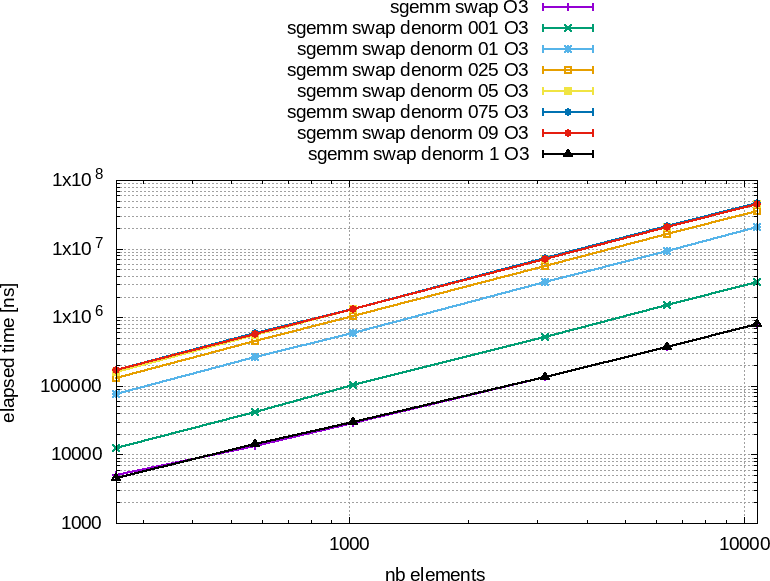
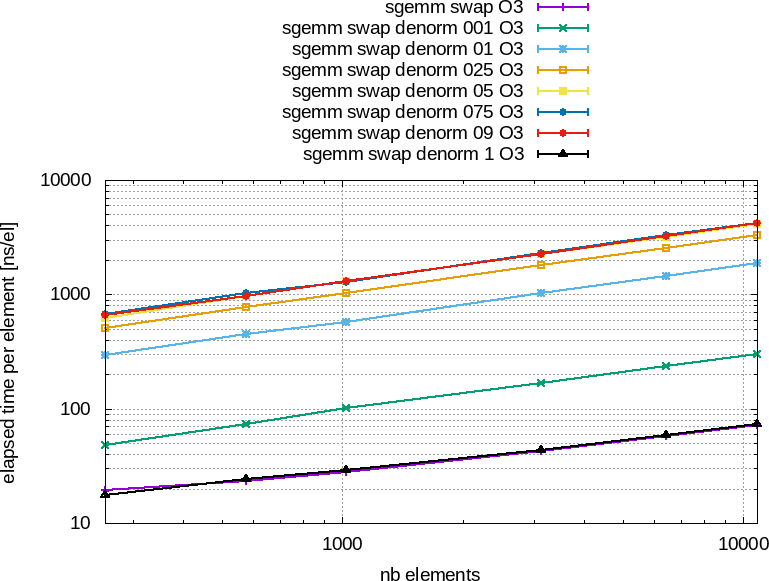
![]() Figure 83 : Performances obtenues avec l'optimisation -O3 entre un produit de matrices de référence (+ violet) et la même fonction mais sur des tableaux initialisés aléatoirement avec des nombres dénormalisés, entre 1 (001) et $100%$ (1).
À gauche, le temps total en nanosecondes en fonctions du nombre d'éléments.
À droite, le temps par élément en nanosecondes en fonctions du nombre d'éléments.
Figure 83 : Performances obtenues avec l'optimisation -O3 entre un produit de matrices de référence (+ violet) et la même fonction mais sur des tableaux initialisés aléatoirement avec des nombres dénormalisés, entre 1 (001) et $100%$ (1).
À gauche, le temps total en nanosecondes en fonctions du nombre d'éléments.
À droite, le temps par élément en nanosecondes en fonctions du nombre d'éléments.
La figure 84 montre les performances avec un produit de matrices vectorisé lorsqu'il traite des tableaux initialisés ou non avec des nombres dénormalisés. On constate que la présence de nombres dénormalisés dégrade fortement les performances quand ceux-ci représentent entre
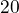 et
et 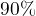 des valeurs traitées.
des valeurs traitées.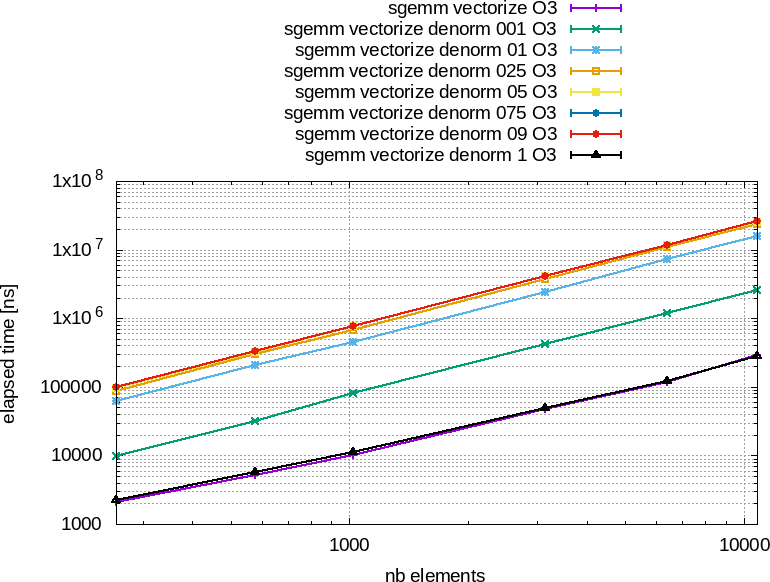
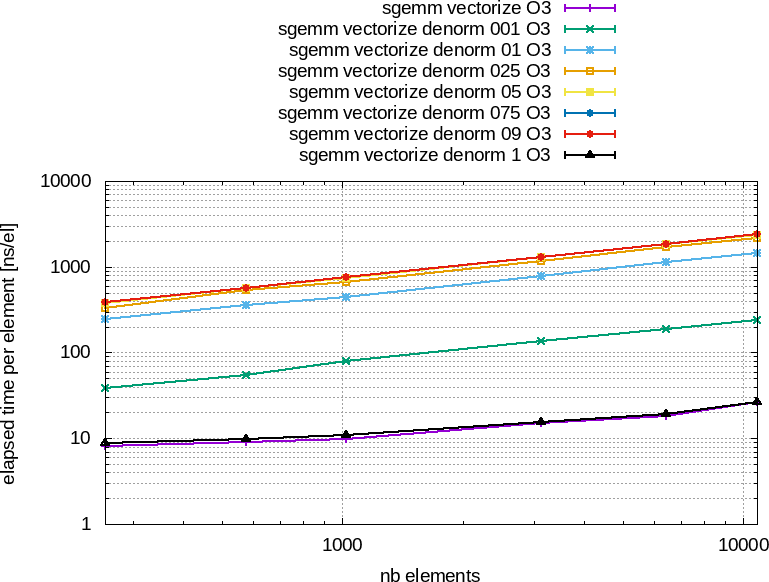
![]() Figure 84 : Performances obtenues avec l'optimisation -O3 entre un produit de matrices vectorisé (+ violet) et la même fonction mais sur des tableaux initialisés aléatoirement avec des nombres dénormalisés, entre 1 (001) et $100%$ (1).
À gauche, le temps total en nanosecondes en fonctions du nombre d'éléments.
À droite, le temps par élément en nanosecondes en fonctions du nombre d'éléments.
Figure 84 : Performances obtenues avec l'optimisation -O3 entre un produit de matrices vectorisé (+ violet) et la même fonction mais sur des tableaux initialisés aléatoirement avec des nombres dénormalisés, entre 1 (001) et $100%$ (1).
À gauche, le temps total en nanosecondes en fonctions du nombre d'éléments.
À droite, le temps par élément en nanosecondes en fonctions du nombre d'éléments.
La figure 85 montre les performances avec un produit de matrices en fonction intrisèques lorsqu'il traite des tableaux initialisés ou non avec des nombres dénormalisés. On constate que la présence de nombres dénormalisés dégrade fortement les performances quand ceux-ci représentent entre
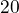 et
et 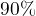 des valeurs traitées.
des valeurs traitées.

![]() Figure 85 : Performances obtenues avec l'optimisation -O3 entre un produit de matrices en fonctions intrisèques (+ violet) et la même fonction mais sur des tableaux initialisés aléatoirement avec des nombres dénormalisés, entre 1 (001) et $100%$ (1).
À gauche, le temps total en nanosecondes en fonctions du nombre d'éléments.
À droite, le temps par élément en nanosecondes en fonctions du nombre d'éléments.
Figure 85 : Performances obtenues avec l'optimisation -O3 entre un produit de matrices en fonctions intrisèques (+ violet) et la même fonction mais sur des tableaux initialisés aléatoirement avec des nombres dénormalisés, entre 1 (001) et $100%$ (1).
À gauche, le temps total en nanosecondes en fonctions du nombre d'éléments.
À droite, le temps par élément en nanosecondes en fonctions du nombre d'éléments.