4.3.1 : Comment rendre vectorisable notre calcul ?
C'est souvent la question l'a plus importante (une fois que l'on a réglé toutes les autres, I/O, formats de données, algorithmes, etc.).
Nottons que les possibilité d'avoir un résultat plus rapidement sont grandes sans se cassez la tête avec des fonctions intrinsèques :
Ici, on veut quand même se mettre dans un cas où on ne va pas ratiboiser la précision du calcul pour gagner du temps. Du genre, on augmente suffisament l'intervalle de temps, on vire les images intermédiares et on gagne un facteur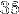 .
Il est bien d'avoir ces idées en tête mais ce n'est pas le propos du moment...
.
Il est bien d'avoir ces idées en tête mais ce n'est pas le propos du moment...
- On pourrait par exemple augmenter les pas de temps et diminiuer le nombre d'images intermédiares que l'on calcul
- Ou diminuer la taille des images
- Calculer les images avec des blocs (pour une fois nous n'avons pas encore parlé de cache dans ce cours mais ça viendra plus tard ne vous inquiétez pas)
Ici, on veut quand même se mettre dans un cas où on ne va pas ratiboiser la précision du calcul pour gagner du temps. Du genre, on augmente suffisament l'intervalle de temps, on vire les images intermédiares et on gagne un facteur
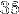 .
Il est bien d'avoir ces idées en tête mais ce n'est pas le propos du moment...
.
Il est bien d'avoir ces idées en tête mais ce n'est pas le propos du moment...
La question est : que faire lorsque l'on est face à un mur et que même le compilateur n'arrive pas à nous aider ?
Réponse : on fait exploser le mur et on aide le compilateur notej'aime bien la pyrotechnie..
Si on résume la situation, le compilateur n'arrive pas a vectoriser correctement car les valeurs que l'on traite sont :
- soit contigûes mais pas ou peu alignées
- soit pas contigûes du tout
Dans les deux cas la vectorisation va mal se passer.
Le problème est donc :
Comment faire pour que les valeurs dans un registre vectoriel soient toutes voisines de celles dans le registre vectoiel voisin du premier ?
Si nos registres vectoriels sont de taille
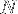 , une méthode, un peu bourin certes, pourrait être de calculer
, une méthode, un peu bourin certes, pourrait être de calculer 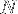 réactions en même temps avec
réactions en même temps avec 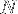 conditions initiales.
C'est bien d'y penser mais on va consommer
conditions initiales.
C'est bien d'y penser mais on va consommer 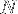 fois plus de mémoire et ça ne nous arrange pas si on veut optimiser un seul calcul.
fois plus de mémoire et ça ne nous arrange pas si on veut optimiser un seul calcul.Il faut que nous construisions une matrice où chaque vecteur de
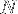 valeurs à des vecteurs voisins qui contiennent les valeurs voisines du précédent.
valeurs à des vecteurs voisins qui contiennent les valeurs voisines du précédent.La figure 6 montre comment modifier une matrice pour satisfaire cette condition pour des registres vecotriels de
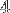 éléments.
éléments.![]() Figure 6 : Comment réordonner les valeurs d'une matrice $16\times 6$ pour que chaque vecteur de $4$ élements contiennent les voisins de ses voisins.
Figure 6 : Comment réordonner les valeurs d'une matrice $16\times 6$ pour que chaque vecteur de $4$ élements contiennent les voisins de ses voisins.
Donc, pour utiliser une vectorisation de taille
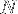 dans notre matrice de départ:
dans notre matrice de départ:- on découpe la matrice en $N$ blocs sur le nombre de lignes
- on entrelace les colonnes en alignant les lignes (toutes les premières lignes des blocs seront dans la première ligne finale, et ainsi de suite)
- on duplique la première ligne et on la colle en bas en la décallant à gauche pour que les dernières lignes des blocs aient leur valeurs du dessous
- on duplique la dernière ligne et on la colle en haut en la décallant à droite pour que les première lignes des blocs aient leur valeurs du dessus
- on ajoute des zéros sur la nouvelle première ligne pour que les voisins du dessus de la première ligne du premier bloc soient des $0$ (pas de voisin du dessus)
- on ajoute des zéros sur la nouvelle dernière ligne pour que les voisins du dessous de la dernière ligne du dernier bloc soient des $0$ (pas de voisin du dessous)
- si le nombre de lignes de la matrice initiale n'est pas un multiple de la taille des registres vectoriels alors il faut aussi mettre des $0$ pour finir les colonnes du dernier bloc (qui sera plus petit que les autres)
Dans notre cas, la valeur 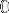 est une valeur dite de padding. Nous utilisons
est une valeur dite de padding. Nous utilisons 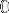 qui est une valeur neutre pour la multiplication, l'addition et la soustraction.
Mais dans le cas d'un calcul utilisant une division, nous utiliseront plutôt la valeur
qui est une valeur neutre pour la multiplication, l'addition et la soustraction.
Mais dans le cas d'un calcul utilisant une division, nous utiliseront plutôt la valeur 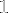 comme padding qui est neutre pour la division.
comme padding qui est neutre pour la division.
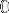 est une valeur dite de padding. Nous utilisons
est une valeur dite de padding. Nous utilisons 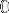 qui est une valeur neutre pour la multiplication, l'addition et la soustraction.
Mais dans le cas d'un calcul utilisant une division, nous utiliseront plutôt la valeur
qui est une valeur neutre pour la multiplication, l'addition et la soustraction.
Mais dans le cas d'un calcul utilisant une division, nous utiliseront plutôt la valeur 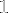 comme padding qui est neutre pour la division.
comme padding qui est neutre pour la division.
Cette méthode est un peut bancale si la matrice a moins de 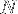 lignes et d'une manière générale elle sera très efficace sur une matrice qui a beaucoup de lignes car le coût de synchronisation de la première et de la dernière ligne sera proportionnellement plus faible.
lignes et d'une manière générale elle sera très efficace sur une matrice qui a beaucoup de lignes car le coût de synchronisation de la première et de la dernière ligne sera proportionnellement plus faible.
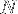 lignes et d'une manière générale elle sera très efficace sur une matrice qui a beaucoup de lignes car le coût de synchronisation de la première et de la dernière ligne sera proportionnellement plus faible.
lignes et d'une manière générale elle sera très efficace sur une matrice qui a beaucoup de lignes car le coût de synchronisation de la première et de la dernière ligne sera proportionnellement plus faible.