Part 5 : Une approche plus subtile
- 5.1) Découpage par blocs
- 5.2) Approche subtile : performance avec des blocs simples
- 5.3) Approche encore plus subtile : performance avec des blocs liés
- 5.4) Peformance du programme avec des blocs liés
- 5.5) Parallélisation avec des blocs liés
Si nous résumons la situation, nous avons un programme de calcul naïf qui nous sert de référence pour le temps de calcul. Et nous avons un programme, écrit avec des fonctions intrinsèques, qui devrait théoriquement aller près de
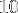fois plus vite que le précédent et qui n'est que 
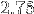fois plus rapide.On pourait se dire que notre test de performance élémentaire (ou micro-benchmark) était très biaisé et que les performances sont ce qu'elles sont. Mais il faut reconnaître que ce n'est pas une approche très scientifique...
Dans l'épisode précédent : Intuitivement, et comme les temps de calcul par éléments sont constants, on peut dire que c'est parce que notre problème est mémory band...
Si nous reprennons nos résulats précédents de la figure 7 que nous rappellons dans la figure 8.
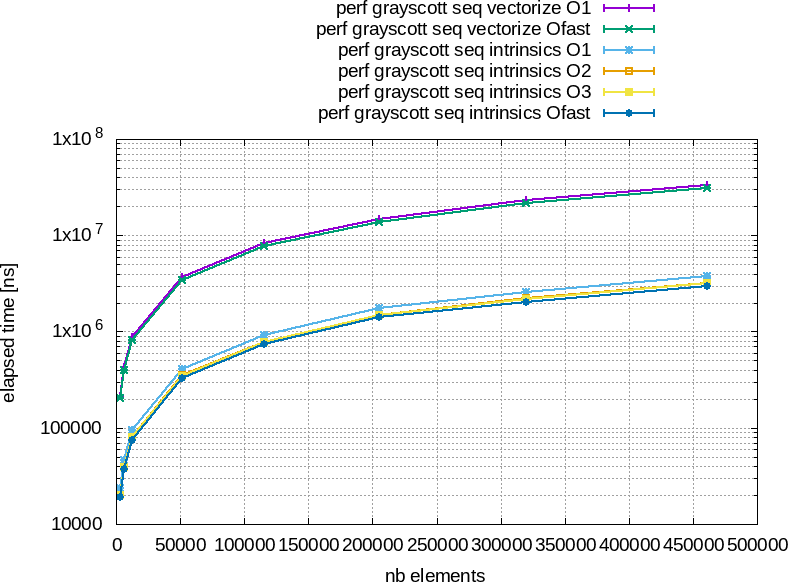
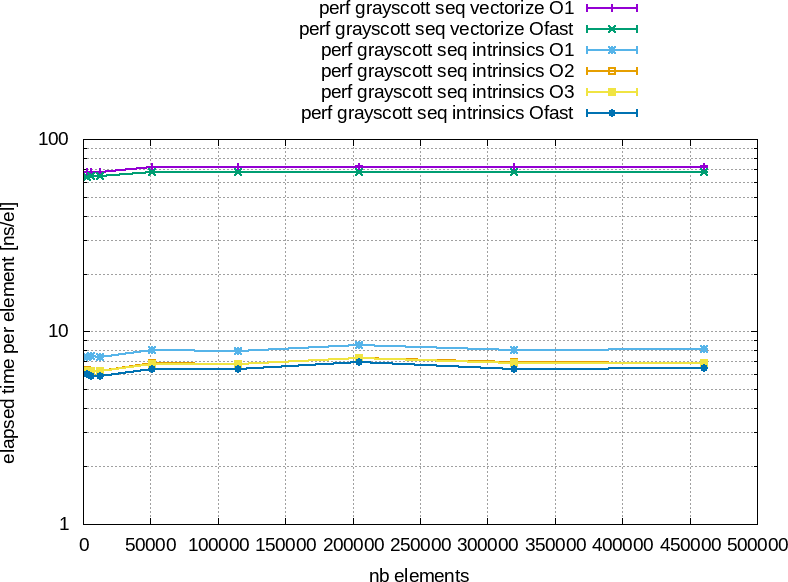
Figure 8 : À gauche : temps total d'éxécution en fonction du nombre d'éléments à traiter. À droite : temps moyen pour traiter un élément en nano-seconde an fonction du nombre total d'éléments à traiter.
On remarque que le temps par élément à droite est relativement constant de
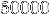à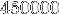 
éléments.
Comme nos éléments sont des float qui ont une taille de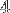 
octets cela représente de 
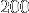ko à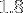 
Mo, donc elles de justesse dans le cache L2 (taille 256 ko) et plus génralement dans le cache L3 (taille 
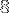Mo).Si on regarde les temps d'accéès des données (du cours How to optimize computation with HPC) :
- Cache L1 : 1 cycle
- Cache L2 : 6 cycles
- Cache L3 : 10 cycles
- RAM : 25 cycles
Sur un ordinateur qui à une fréquence d'horloge de
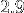GHz cela revient à :- Cache L1 : 1 cycle ($0.34$ ns)
- Cache L2 : 6 cycles ($2.07$ ns)
- Cache L3 : 10 cycles ($3.45$ ns)
- RAM : 25 cycles ($8.62$ ns)
or, nous avions des images en full hd soit
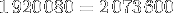pixels soit 
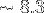Mo (ou exactement 
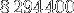octets).Or, nous pouvons vérifier la taille du cache (le votre est peut-être différent mais cela doit être cohérent avec votre temps de calcul) :
cat /proc/cpuinfo | grep "cache size" cache size : 8192 KB cache size : 8192 KB cache size : 8192 KB cache size : 8192 KB cache size : 8192 KB cache size : 8192 KB cache size : 8192 KB cache size : 8192 KB
Il y a une valeur par thread CPU.
Là, on se dit que c'est ballot, car nos images ne rentrent pas le cache L3, elles sont donc en RAM. Donc le rapatriment de ces données prendrait environ
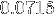seconde par images ce qui explique une bonne partie du temps de calcul d'une image qui est d'environ 
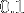seconde avec la version en fonctions intrinsèques.